Swimmers are a classic example of interacting active matter. First, they need a constant input of energy to keep them swimming. Second, they can interact through the fluid: each swimmer disturbs the fluid by swimming through it, which in turn affects other swimmers, resulting in rich collective behaviors. Furthermore, both these aspects can be worked out, to a certain extent, from more fundamental principles, i.e. fluid mechanics.

Much attention has been devoted, in particular, to microscopic swimmers: bacteria such as E. Coli, algae such as Chlamydomonas reinhardtii, sperm cells, and a variety of artificial micro-swimmers inspired by their living counterparts. Because they are small and slow, their dynamics is dominated by viscosity, which greatly simplifies analytical studies of their interactions with the fluid.

Some of these swimmers, instead of swimming in a straight line, rotate around themselves. A remarkable property of such rotors is that they can create azimuthal flow fields that lead to azimuthal interactions between particles. The nature of this flow field, however, depends critically on the source of rotation. In fact, the azimuthal flow field that has been observed around particles that are driven to rotate by an external torque is no longer present when rotation is obtained through internal processes, i.e. as a result of the swimmer pushing on the surrounding fluid. We showed, however, that such internally driven rotors still exhibit an azimuthal interaction much similar to that experienced by externally driven ones, but with a faster decay (1/r4 instead of 1/r2 for a liquid-air interface).

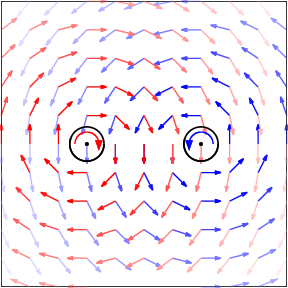
One important consequence of the existence of an azimuthal interaction is the possibility to form self-propelled pairs, i.e. pairs of rotors rotating in opposite directions that push each other in a common direction.